491 words
2 minutes
两次插值构建三维速度模型
在三维地震成像中通常需要构建三维初始模型,这些模型往往来自已有的公共速度模型或其他前人研究,尽管提供的模型多为规则网格,由于我们所需网格大小是自定义的,所以需要对其进行网格化。而网格化所用的插值算法多为线性插值,它存在一个弊端:如果我们的网格范围比原先的大,将会出现NaN结果,无法用于后续计算。
本文介绍通过两次插值的方法解决这一问题。
1. 将原始模型线性插值到自定义网格
第一次插值,即将原始模型数据假设为散点,在Python用scipy.interpolate.griddata线性插值进行网格化。
import numpy as npfrom scipy.interpolate import griddata
new_dep, new_lat, new_lon = np.meshgrid(dep, lat, lon, indexing='ij')grid_vp = griddata( points[:, 0:3], points[:, 3], (new_dep, new_lat, new_lon), method='linear')这里dep, lat和lon为所需网格深度、纬度和经度方向的坐标,均为一维数组。points是原始模型数据,共4列,分别为深度、纬度、经度和数值。griddata函数对于超过原始模型范围的网格点默认会返回NaN值。
线性插值后的结果如图。黄色区域即为NaN值区域,这样的模型不能满足后续的计算需求。
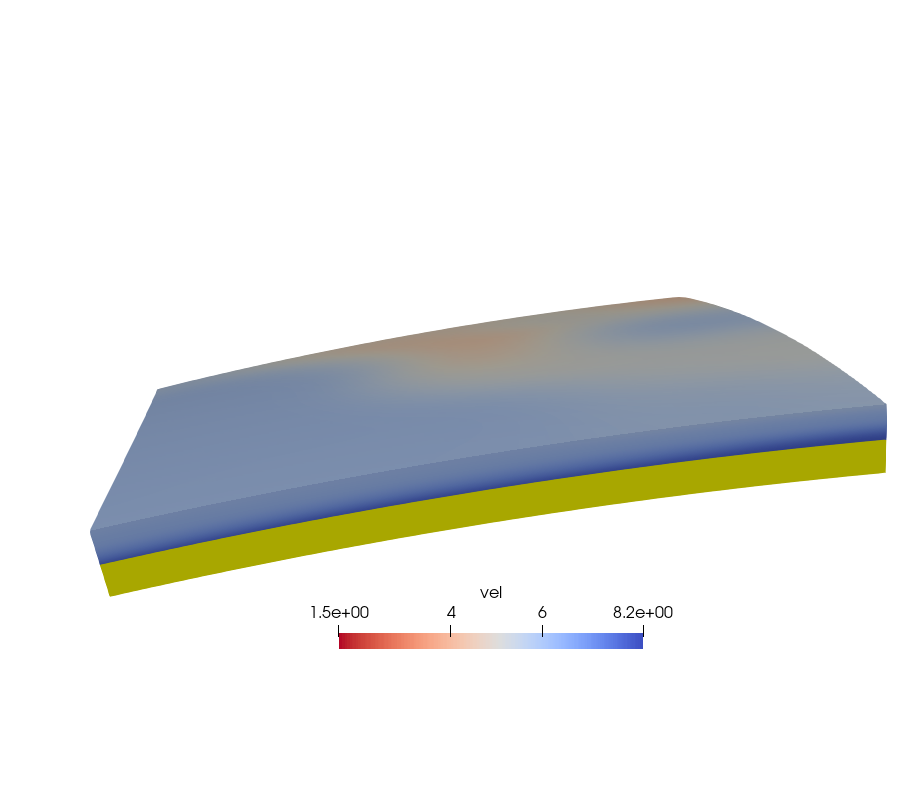
2. 用临近点插值将NaN值点赋值
这里用到第二次插值,利用临近点插值 (Nearest Interpolation) 进行外插,填补空值点,同时保证数值不会偏离正常值。这里的思路是将非空值点取出当作散点,用相同的网格进行临近点插值。
def ignore_nan_val(data): index = np.where(~np.isnan(data)) values = data[index] points = np.array(index).T zidx = np.arange(data.shape[0]) yidx = np.arange(data.shape[1]) xidx = np.arange(data.shape[2]) zz, xx, yy = np.meshgrid(zidx, yidx, xidx, indexing='ij') interpolated = griddata( points, values, (zz, xx, yy), method='nearest' ) return interpolated.reshape(data.shape)两次插值之后的结果如下图,NaN值部分已经由最底层速度填补。
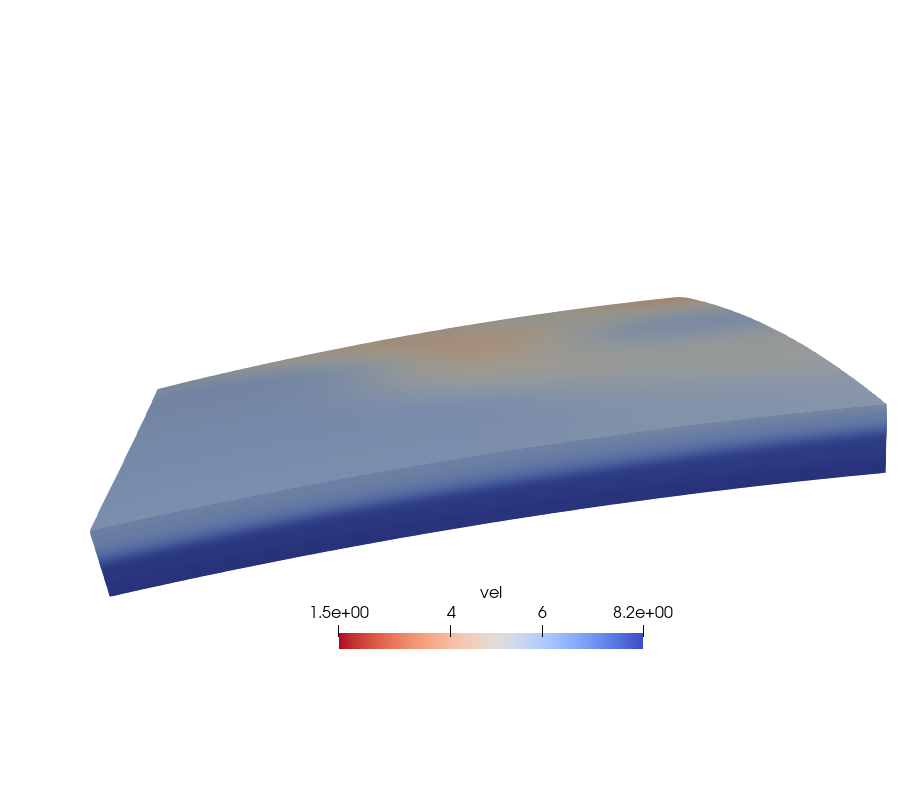
两次插值构建三维速度模型
https://blog.xumijian.me/posts/double_interp/